- 您現(xiàn)在的位置:買賣IC網(wǎng) > PDF目錄383339 > MAX1870A (Maxim Integrated Products, Inc.) Step-Up/Step-Down Li+ Battery Charger PDF資料下載
參數(shù)資料
| 型號(hào): | MAX1870A |
| 廠商: | Maxim Integrated Products, Inc. |
| 英文描述: | Step-Up/Step-Down Li+ Battery Charger |
| 中文描述: | 升/降壓型Li+電池充電器 |
| 文件頁數(shù): | 23/32頁 |
| 文件大小: | 1091K |
| 代理商: | MAX1870A |
第1頁第2頁第3頁第4頁第5頁第6頁第7頁第8頁第9頁第10頁第11頁第12頁第13頁第14頁第15頁第16頁第17頁第18頁第19頁第20頁第21頁第22頁當(dāng)前第23頁第24頁第25頁第26頁第27頁第28頁第29頁第30頁第31頁第32頁
M
Step-Up/Step-Down
Li+ Battery Charger
______________________________________________________________________________________
23
effectively cut in half to allow for both the step-up cycle
and the step-down cycle. The switching frequency is
typically between 350kHz and 405kHz for V
IN
between
8V and 28V. See the
Typical Operating Characteristics
.
Compensation
Each of the three regulation loops (the battery voltage,
the charge current, and the input current limit) are com-
pensated separately using the CCV, CCI, and CCS
pins, respectively. Compensate the voltage regulation
loop with a 10k
resistor in series with a 0.01μF capaci-
tor from CCV to GND. Compensate the charge current
loop and source current loop with 0.01μF capacitors
from CCI to GND and from CCS to GND, respectively.
Voltage Loop Compensation
When regulating the charge voltage, the MAX1870A
behaves as a current-mode step-down or step-up
power supply. Since a current-mode controller regulates
its output current as a function of the error signal, the
duty-cycle modulator can be modeled as a GM stage
(Figure 9). Results are similar in step-down, step-up, or
step-up/down, with the exception of a load-dependent
right-half-plane zero that occurs in step-up mode.
The required compensation network is a pole-zero pair
formed with C
CV
and R
CV
. C
CV
is chosen to be large
enough that its impedance is relatively small compared
to R
CV
at frequencies near crossover. R
CV
sets the
gain of the error amplifier near crossover. R
CV
and
C
OUT
determine the crossover frequency and, there-
fore, the closed-loop response of the system and the
response time upon battery removal.
R
ESR
is the equivalent series resistance (ESR) of the
charger’s output capacitor (C
OUT
). R
L
is the equivalent
charger output load, R
L
=
V
BATT
/
I
CHG
= R
BATT
.
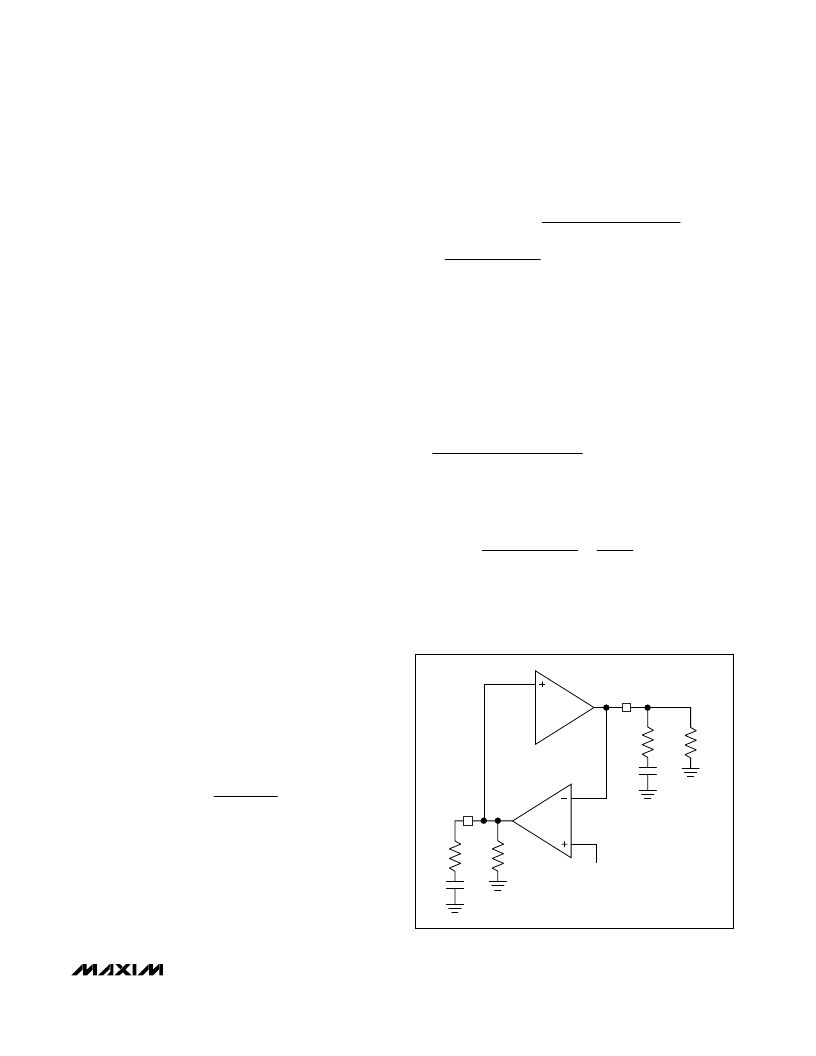
The equivalent output impedance of the GMV amplifier,
R
OGMV
, is greater than 10M
. The voltage loop
transconductance (GMV =
I
CCV
/
V
BATT
) scales
inversely with the number of cells. GMV = 0.1μA/mV for
four cells, 0.133μA/mV for three cells, and 0.2μA/mV for
two cells. The DC-DC converter’s transconductance
depends upon the charge current-sense resistor RS2:
where A
CSI
= 18, and RS2 = 30m
in the
Typical
Application Circuits
, so GM
PWM
= 1.85A/V.
Use the following equation to calculate the loop transfer
function (LTF):
The poles and zeros of the voltage-loop transfer func-
tion are listed from lowest frequency to highest frequen-
cy in Table 3.
Near crossover, C
CV
has much lower impedance than
R
OGMV
. Since C
CV
is in parallel with R
OGMV,
C
CV
dom-
inates the parallel impedance near crossover.
Additionally, R
CV
has a much higher impedance than
C
CV
and dominates the series combination of R
CV
and
C
CV
, so:
C
OUT
also has a much lower impedance than R
L
near
crossover, so the parallel impedance is mostly capaci-
tive and:
If R
ESR
is small enough, its associated output zero has
a negligible effect near crossover and the loop transfer
function can be simplified as follows:
R
sC
x R
sC
L
OUT
L
OUT
(
)
1
1
+
R
x
sC
sC
x R
x R
R
near crossover
OGMV
(
1
CV
CV
CV
OGMV
CV
(
)
)
,
1
+
+
LTF
GM
xR
x
sC
x R
R
sC
x
R
sC
x R
x G
x
sC
x R
PWM
OGMV
(
1
CV
CV
)
CV
OGMV
L
OUT
L
MV
OUT
ESR
=
+
+
+
+
(
)
(
)
(
)
1
1
1
GM
A
x RS
PWM
CSI
=
1
2
GM
OUT
REF
GMV
R
L
R
ESR
C
OUT
R
O
R
CV
C
CV
BATT
CCV
Figure 9. CCV Simplified Loop Diagram
相關(guān)PDF資料 |
PDF描述 |
|---|---|
| MAX1870AETJ | Step-Up/Step-Down Li+ Battery Charger |
| MAX1873 | Simple Current-Limited Switch-Mode Li Charger Controller |
| MAX1873SEEE | Simple Current-Limited Switch-Mode Li Charger Controller |
| MAX1873REEE | Simple Current-Limited Switch-Mode Li Charger Controller |
| MAX1873TEEE | Simple Current-Limited Switch-Mode Li Charger Controller |
相關(guān)代理商/技術(shù)參數(shù) |
參數(shù)描述 |
|---|---|
| MAX1870AETJ | 功能描述:電池管理 RoHS:否 制造商:Texas Instruments 電池類型:Li-Ion 輸出電壓:5 V 輸出電流:4.5 A 工作電源電壓:3.9 V to 17 V 最大工作溫度:+ 85 C 最小工作溫度:- 40 C 封裝 / 箱體:VQFN-24 封裝:Reel |
| MAX1870AETJ+ | 功能描述:電池管理 Li+ Step Up/Step Down Battery Charger RoHS:否 制造商:Texas Instruments 電池類型:Li-Ion 輸出電壓:5 V 輸出電流:4.5 A 工作電源電壓:3.9 V to 17 V 最大工作溫度:+ 85 C 最小工作溫度:- 40 C 封裝 / 箱體:VQFN-24 封裝:Reel |
| MAX1870AETJ+T | 功能描述:電池管理 Li+ Step Up/Step Down Battery Charger RoHS:否 制造商:Texas Instruments 電池類型:Li-Ion 輸出電壓:5 V 輸出電流:4.5 A 工作電源電壓:3.9 V to 17 V 最大工作溫度:+ 85 C 最小工作溫度:- 40 C 封裝 / 箱體:VQFN-24 封裝:Reel |
| MAX1870AETJ-T | 功能描述:電池管理 RoHS:否 制造商:Texas Instruments 電池類型:Li-Ion 輸出電壓:5 V 輸出電流:4.5 A 工作電源電壓:3.9 V to 17 V 最大工作溫度:+ 85 C 最小工作溫度:- 40 C 封裝 / 箱體:VQFN-24 封裝:Reel |
| MAX1870AEVKIT | 功能描述:電源管理IC開發(fā)工具 Evaluation Kit for the MAX1870A RoHS:否 制造商:Maxim Integrated 產(chǎn)品:Evaluation Kits 類型:Battery Management 工具用于評(píng)估:MAX17710GB 輸入電壓: 輸出電壓:1.8 V |
發(fā)布緊急采購,3分鐘左右您將得到回復(fù)。